THE PRESELI CONNECTION
PART THREE of the STONEHENGE – WOODHENGE tryptych
INTRODUCTION
Part One and Two of this tryptych revealed an unexpected geometrical relationship between the location of Stonehenge and that of its sister henge monument, Woodhenge. Part Three now expands this new evidence. By comparing data from the megalithic landscape around Stonehenge/ Woodhenge with that from the megalithic landscape in and around the Preseli Hills of West Wales a new type of connection emerges, one that links the ‘bluestone’ culture of the Preseli Hills of West Wales with that of the Wessex culture, specifically the Stonehenge landscape shown above (but perhaps even Avebury and elsewhere).
In Part One & Two, Stonehenge and its sister Woodhenge were shown to be geometrically connected. A line joining the location of their respective centres defines an azimuth angle or bearing identical to the smallest angle of a 5:12:13 right angled triangle (a so-called Pythagorean triangle). The line becomes the ’13’ side. The other two sides, the ‘5’ and the ’12’ side are therefore be aligned to the cardinal points of the compass.
[The azimuth angle of the hypotenuse with respect to an east-west line is identical to the angle of geometry of a 5:12:15 triangle – 22.619 degrees.]
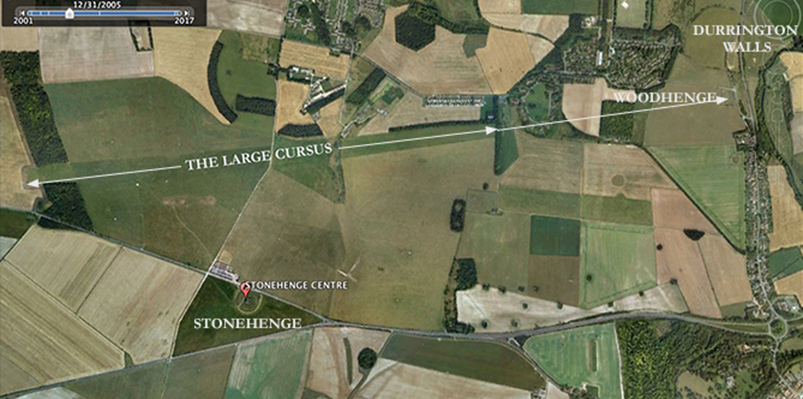
The distance or measurement between the centres of these two major monuments was found to present the recogniseable and familiar geometrical and metrological patterns that have been found elsewhere when megalithic sites, when the line connecting them is measured. A map of the broader landscape around Stonehenge is shown below (Figure One), with the azimuths of the midsummer sunrise and major standstill moonset (e+i) marked for 2600 BC.
Figure One – The Landscape around Stonehenge
The Bluestone Monologues
In 1923, geologist H H Thomas discovered that the bluestones originated from outcrops in the Preseli mountains in Pembrokeshire, Wales, some 135 miles as the archaeopteryx flies from Stonehenge. How they got to Salisbury plain remains somewhat contentious, some experts preferring glacial over human action. Neither camp can prove the case, and the whole argument has become mired through lack of the necessary discovery of any remains of a prehistoric boat, sledge or rollers!
Since the 1920s, various improved petrological analyses taken from outcrops on or near the main Preseli ridge have shown the local ophitic dolorite (feldspar-spotted bluestone to the layman) to provide a close match with many of the larger bluestones found at Stonehenge.
Other recent archaeological research has reversed the thinking of the past century by now suggesting what some other researchers, including myself and John North, had thought pretty obvious all along – that the 56 Aubrey holes may once have held a circle of bluestones. Archaeologists have accounted for over 80 bluestones within the later structures at Stonehenge, this would be more than enough to fill the Aubrey holes.
Closure on the bluestone argument, one way or the other, would be a big relief to many researchers into Stonehenge’s hoary history, and doubly so for the poor layman saturated with dull documentaries that fail to settle the matter one way or the other. However, the glacial flux/ human transportation argument is not the matter I am most interested in settling within this article. For my particular type of research concerning megalithic culture this hoary old argument is simply not relevant, and anyway it happens not to be the main question that needs answering.
THE BLUESTONE DEBATE
Making such a comparison between the astronomical, geometrical and metrological similarities between megalithic sites in the Preseli region and those located on the Stonehenge landscape reveals a new and unexpected cultural link that once existed between the bluestone outcrop sites and Stonehenge. Those factions in archaeology and geology who presently have not been able to prove whether or not the bluestones arrived at Stonehenge by the action of glacial flux or by the intentional act of human transportation are thereby offered an independent and valuable new data source.
It remains the case that neither party in the glaciation/human transportation argument has yet provided the necessary evidence required to demonstrate how (or why) the bluestones appear to have been so crucial to the builders of Stonehenge. For at least ten years I have stood back from this debate, my developing methodology enabling me to effectively put aside the ‘bluestone question’ altogether. Instead, a developing methodology has shown that Stonehenge, Woodhenge and the Preseli Hills are connected through the same cultural ideology, the same cosmological model that developed through incorporating an identical megalithic technology, based on the same component sciences, into a transportable package, a moveable feast. This package could readily be taken anywhere in the megalithic world, and it did not necessarily need to involve moving large megaliths over unfeasible distances.
How the bluestones originated on site at Stonehenge is thus given a long overdue rest, and the question no longer stands in the way of understanding Stonehenge and its relationship with the bluestone outcrops in the Preseli Hills. The primary question should in any case always have been why and not how the bluestones arrived at Stonehenge, but no professional archaeologist has ever grabbed hold of this more pertinent question by the throat, let alone offered any credible answers.
DEVELOPING A METHODOLOGY FOR ANALYSING MEGALITHIC SITES
I have a second purpose in introducing students of megalithic science to this comparison. It introduces a new and simply applied methodology that can be applied when undertaking megalithic research at any other major megalithic sites. By ‘reverse engineering’ the same methodology as appears to have been used by the original monument builders, new channels for understanding the mind-set of the megalithic builders are opened, and this reveals their capabilities. Such a claim may be quite shocking for upholders of the present cultural model of Neolithic Europe. For everyone else, it will be found uplifting, reconnecting us to a long lost legacy from the Stone Age, connecting into the minds of prehistoric ‘megalithic scientists’ aka the astronomer-priests of 1970s archaeology textbooks aka the ‘Druids’ of Stukely’s day.
The methodology demonstrated here displays something of the megalith builder’s priorities, their methods and even their capability to reduce errors of measurement. As a side dish this offers the researcher a practical suggestion as to how useful and accurately made astronomical observations could have been stored over long periods of time.
1. THE AXIOMS
There are six assumptions/ axioms that were adopted during the research programme. Some of these are not new.
1. That ropes and rods were used to measure point to point across significantly large distances overground between megalithic monuments.
2. That these distances were often ‘lengths of time’ and used to record time periods, such a the length of the lunar month or the solar year.
3. That the culture possessed accurate and easily applied techniques for measuring lengths.
4. That the end point locations were often marked or monumentalised with stone structures.
5. That the structures in 4 provided built in standards of key lengths in order to facilitate 1 to 4 above, such as to provide calibration methods to enable long term storage of astronomical or geodetic records, and absolute or reference measures.
6 That the measurable accuracy was accurate to 99.9% or 1 part in a thousand.
Some elaboration with regard to this listing may now prove useful:
1 & 2. Lengths of Time
It is first suggested that long ropes were employed by the megalith builders, together with shorter rods, and that these were marked up with the key time periods of the sun, moon and lunar nodes, based on long-term observations. In other words, these ropes (and rods) were intended to represent lengths of time. The salient lengths required to facilitate and then record astronomical observations (taken over long periods of time, and sometimes over many generations) were then incorporated within the key structural features of the most significant temple monuments, to become their principal dimensions. The monuments thereby stored key astronomical constants as lengths, records that were memorialised or enshrined within the monuments themselves. Large stones endured where wooden posts and ropes would not endure. The employment of megalithic structures marked immoveable locations which then offered the possibility of maintaining accurate standards of length for use within a far wider community over long periods of time.
2. Measuring lengths
All the lengths undertaken in the analysis that follows are ground lengths obtained from Google Earth, rounded up to the nearest foot unless stated otherwise. The azimuth angle between two sites is regarded as a straight line (originally a pegged rope) that connects two sites together. In the research, this line was draw on the landscape using Google Earth, and its length and azimuth angle recorded.
This method of determining lengths was chosen not only because it is simple and adequately accurate for the purposes in hand, but also because it can be checked and agreed upon by almost any educated modern person who owns a computer connected to the web. Google Earth has transformed the subject matter here because it removes the arduous and frankly tedious nature of surveying and measuring over often difficult territories. Direct point-to-point measurement is a fundamental measurement that is dependable over shorter distances where it can be accurately undertaken, independent of the effects of the size of the earth or its shape.
Accurate terrestrial measurement over larger distances – tens of miles – has to compensate slightly for the effects of the curvature of the earth and eventually even for the individual tiny changes from perfect sphericity that occur in different regions of the world. Mercifully, the distances involved in this research are small enough to render these effects negligible. In other words, because we are dealing with relatively small distances, there is no requirement to compensate for the curve of the earth, nor resort to using spherical geometry.
The now rather dated technique of taking latitude and longitude measurements of two points on an Ordnance Survey map and, from these, calculating their distance apart, is capable of delivering the same length as does direct measurement with long ropes, or the use of Google Earth. Often, however, it does not, and there are scientific reasons for this, beyond the scope of this article. The main reason for this discrepancy is that the geoid (the model of the earth’s shape) used by the OS to model the earth (OSB36) is a little different from that determined by Google Earth (WGS84). Important to note is that It has not been assumed in this article that prehistoric people were able to accurately measure latitude or longitude.
4. Determining end point locations
Where there is no clear positioning marker for one of the ends of a line connecting megalithic structures then the length given is the best estimate possible. Reasons for this include a monument being highly ruinous, or a standing stone having fallen or having moved from its original position. For example, a tree that grows between two stones is capable of pushing them apart before it dies, rots away and leaves no visible evidence of the once powerful forces it once acted on the two stones. Similarly animal burrows can tangible loosen the footings of a stone, eventually causing it to lean or topple. Frost and wind damage, separately or together, can break certain types of stone into pieces over time, and over time, rainfall can dramatically erode limestone and sandstone menhirs. Thom was quick to note that ‘the worst and most deceptive disturbances, however, are those produced by people who re-erect stones without leaving any record; the re-erectors have no knowledge of the original geometry and they have no survey. They simply replace the stone where they think it looks best; examples can be found at Seascale (L1/10, Callanish H1/1, and Killin P1/3‘ (Thom, MRBB, 1978, page 3).
Fully recognising that a priori bias may sway the selection of the ‘most likely’ end point, for these readings I took the precaution of asking for these readings to be taken by several people having no knowledge whatsoever of the subject matter of the ‘experiment’. In these cases an average value was chosen. An accurate ruler and the techniques to employ it correctly will always reduce the error incurred in measuring the distance between two ruinous megalithic sites whose exact original positions are not known with certainty. Such measurements are capable of delivering a more accurate estimate of the intended length (if there ever was an intended length!) than any intended length available from the ruinous monument(s) themselves. How this works in practice will be explored later, after an exploration of what one might expect from ‘accurate measurements’.
6. Accuracy
Accuracies from a perceived ideal or ‘perfect’ fit are (when appropriate) quoted here in parentheses, as percentage errors. Thus, 99% means the error is one part in a hundred. To demonstrate the true capabilities of a stone age culture to measure accurately, one must find examples that are way better than within 1% of any hypothesised value. I have always thought that examples of much better accuracy than ‘within one percent error’ are required to convince anyone that the data is not either coincidental, imagined or serendipidous.
99.9% is one part in a thousand, and this is less than, but approaches, the level of accuracy that Alexander Thom and his son Archie Thom were able to achieve in the field in order to refute the claims being made by some archaeologists during the 1970s that ‘it would be impossible to use wooden rods to measure with accuracy that we (Thom & Thom) claim for the megalithic yard‘.
This comment is quoted in a description of the Thom experiment within Megalithic Remains in Britain and Brittany (MRBB, Oxford, 1978, pp 42-43), where accuracies of one part in almost 3000 were realised with exceptional care, but without using specialised equipment. One part in 1500 could be readily achieved under all circumstances.
One part in 1500 represents an accuracy of better than 99.9%, and to place this in context within the lengths being considered in this article, this level of error in 2.722 feet, (Thom’s revised length of the megalithic yard), suggests an allowable range of measurements for this unit from 2.7193 feet to 2.723 feet.
Should the reader require more information concerning this aspect of the likely accuracies that can be achieved when measuring over relatively short distances using ‘megalithic’ equipment, then the introduction of Megalithic Sites in Britain and Brittany gives much useful information that sets the scene for this article (pp 2 – 4, [1.4 – 1.5]), as also does the biographical account of Thom’s life and work : Alexander Thom: Cracking the Stone Age Code (available from this website).
Finally 99.99% represents an error of one part in ten thousand, an accuracy which, over difficult terrain, would be hard to achieve with either modern or traditional surveying equipment and methods.
5. Absolute or reference measures
During the 1980s I used to lecture on instrumentation techniques. My brighter students soon recognised that to connect the word absolute with measurement immediately presented an oxymoron. Even the most exacting experimental techniques and the best precision engineering skills will always deliver a minute amount of error in any length, area, weight or whatever other physical quantity that is being measured. This phenomenon has a name. Coincidentally, it was first found to occur within quantum physics experiments during the very same year as the Cunninghams were excavating Woodhenge, and it has since become known as Heisenberg’s uncertainty principle, following its discovery by physicist Werner Heisenberg.
THE EXPERIMENT
1. MEASURING THE CURSUS
Some of the background evidence supporting the claims and suggestions that follow can be found in previous works, which I appreciate the more casual reader may not wish to peruse. Such readers may prefer to take note that the ideal kind of environment within which to lay out and compare very long ropes, being marked up with all manner of astronomical and perhaps meteorological time related events, would be a flat ‘runway’ marked out on the landscape by a bank and/or ditch that placed it out of bounds from anyone except those initiated into the knowledge required to operate, mark up and then ‘read back’ these ropes.
One well known and well defined Neolithic monument within the Stonehenge landscape meets these basic requirements very well. It has the name The Large Cursus, and it is nearly two miles long, sited a short distance north of Stonehenge, runs roughly east to west and is clearly visible on Google Earth (see below). A much smaller cursus is located still further to the northwest of Stonehenge and is ruinous, moreover it is far less visible on Google earth. The small cursus monument has therefore been ignored in this work.
Figure Two – The Stonehenge Cursus (courtesy Google Earth).
In the context of this article the large cursus cannot be ignored, for the following reasons:
a). The orientation of the cursus on the landscape aligns its eastern end to Woodhenge. Unfortunately, this interesting fact has been obscured because the eastern end of the cursus has quite recently been abruptly interrupted by modern military housing and recreational building works to the southeast of the army town of Larkhill.
b). The total length of the cursus from its westernmost end to Woodhenge centre is about 13,610 feet. This length may readily be confirmed using Google Earth, although regrettably, there is no convenient stone or marker to mark its westernmost end, just a boundary bank. It is not known where measurements, if any, were taken from. Ground radar may some day suggest that a row of small pegs or posts were once hammered into the chalk subsoil near the end boundary, but until then…well, in the meantime we will have to note that over such a large distance a few feet of indeterminacy at either end introduces only a very small error.
c). Were this length of 13,610 feet intended, (i.e. for the measurers to have achieved ±99.9% accuracy), the spread of measurements could span from 13,596 to 13,623 feet, a range of ± 14 ft.
d). The distance from the westernmost end of the cursus to the famous Cuckoo stone is 12,248 ft (The range at 99.9% is ±12 ft). From the Cuckoo stone to the tangential point of the perimeter of ring III at Woodhenge is 1,361ft in length and lies parallel to the line that connects Woodhenge centre to the westernmost end of the cursus.
There is even a large post hole at the tangential point coincidental with the line projected from the hypotenuse of the 12:35:37 Pythagorean triangle that Alexander Thom demonstrated had been used to define the complex geometry of Woodhenge’s coaxial rings.
2. THE METROLOGY OF THE CURSUS
It is now possible to identify a metrological thread that connects the cursus with both Stonehenge and Woodhenge.
Alexander Thom (1968) originally identified a metrological ‘family’ of units of length that emerged (were revealed) from his surveys at the various types of megalithic circles, stone rows and some more complex designs and landforms. Briefly, the chronology and chronicle of this work is given below:
In Megalithic Sites in Britain, (1968, Oxford) Thom used the not inconsiderable statistical talents of two of the greatest mathematicians of that time, independently of each other, to devise a statistical methodology that would take the data derived from his accurate surveying of over 200 megalithic rings in order to see what unit(s) of length had been employed by their builders, if any, the kind of simple question an engineer would ask, as a matter of course.
The outcome was that the data, taken from circles and rings throughout the length and breadth of Britain, revealed that a length of 5.44 feet having been employed as the ‘quantum’ length in the diameters of the data sample. Thom called it the Megalithic fathom. The unit for the radii of the circles was correspondingly half this value, and this became the notoriously controversial Megalithic yard of 2.72ft, as named by Thom.
Over the following ten years of further research and more survey plans, these units of length were minutely increased, following Thom’s several major surveys at Carnac, in Brittany, France, Brodgar, Stonehenge and Avebury. They were increased by 0.08% and their new values defined in Thom’s last major work, Megalithic Remains in Britain and Brittany (MRBB, 1978, Oxford, pp 40-43). Most of the research was published in a series of articles in The Journal for the History of Astronomy (JHA, various 1970-1975) by its far sighted editor, Mike Hoskins.
The table below lists these measures all linked within a ‘family’:
Megalithic Yard (MY = 40MI) 2.722 feet
Megalithic Fathom (2MY = 80 MI) 5.444 feet
Megalithic Rod (MR = 2.5MY = 100 MI) 6.805 feet
Megalithic Inch (100 MI = MR) 0.8166 inches
Table One. The Megalithic ‘Family’ of Measures identified by Professor Alexander Thom
The megalithic yard was now determined as being of length 2.722 feet, and comprised forty megalithic ‘inches’ of 0.8166 ‘standard or Imperial’ inches. The length of the megalithic inch was identified statistically (and independently) from an analysis of 57 examples of cup and ring marks found throughout the British Isles.
Two megalithic yards then became a megalithic fathom of length 5.444 feet while two and a half megalithic yards defined what Thom termed a megalithic rod (6.805 feet or 100 megalithic inches). The analysis of this ‘family’ of revealed megalithic units appears in chapters four and five of MRBB.
As one of Thom’s critics has pointed out, in All Done with Mirrors, (John Neal, Secret Academy Press, 2000) Thom’s nomenclatures for his claimed unit family were incorrect, misaligned from known ancient practice within metrology. Neal’s objection is valid but it presupposes that the system of ancient metrology was perfected, and up and running, during Neolithic times, which is presently not possible to establish.
However, Neal has a fair point. Had Thom better understood the ancient system of metrology he would have recognised that a ‘yard’ is always three times the foot from which it derives. Thus, because the eponymous megalithic yard is not three feet in length, being nearer two and half times its root ‘foot’ (just!), a multiplier (x 2.5) that, in metrology, is called a step. The megalithic fathom is then seen to be a pace (two steps).
To be correctly within the ‘bandwidth’ of the traditional length of Thom’s rod measure (16.5 feet) one must multiply its length by 2.42. Thom’s ‘rod’ is thus nowhere near the length of any traditional rod measure, and its naming is anomalous.
3. THE METROLOGY OF THE CURSUS
The length of the large cursus, between its somewhat indeterminate western end and the centre of Woodhenge, measures somewhere between 13,590 and 13,612 feet, and the upper value fits Thom’s units well, for,
13,610 feet = 5000 megalithic yards (MY)
= 2500 megalithic fathoms (MF)
= 2000 megalithic rods (MR),
and 2000 MR x 100 = 200,000 megalithic inches (MI)
Table Two. The length of the Large Cursus expressed in Thom’s family of units.
This length, 13,610 feet, therefore lies within 99.985% of fitting into all categories of Thom’s discovered ‘family’ of megalithic units, each an integer number multiplied by powers of ten.
The sole ‘experimental technique’ in this research has been to accurately measure various lengths, using Google Earth in lieu of the more traditional rods, pegs, ropes and calibrated rulers. The result suggests the cursus may itself have been a giant ruler, calibrated in the same megalithic units that Thom independently discovered elsewhere, in the diameters and perimeter lengths of stone circles, ellipses and rings. These units were revealed to Thom through hundreds of painstaking (and precise) surveys between 1934 and 1977, none of which included the cursus. So, can it now be reasonably proposed that this unexpected correlation presented above was intentional, part of the prehistoric design of this presently rather neglected landform?
It is helpful at this point to introduce another length, this being the distance between the western end of the cursus and the well known Cuckoo stone, a large sarsen boulder often visited and recognised as a component part of the Stonehenge landscape. That distance is 4500 megalithic yards, and this makes the distance from the Cuckoo stone to Woodhenge 500 megalithic yards. This measurement fits neatly within the other qualitative and quantative properties of the landforms discussed elsewhere.
Are these findings a bizarre coincidence, a serendipidous match, or do they represent an intentional quality of the cursus? I would suggest the latter option if only because the ensuing results appear, to an engineer, to be unlocking a design process. But what was that design all about, what was it for?
Thom’s original survey plan of Woodhenge gave perimeters for its ever increasing complex geometrical rings in integer values of megalithic yards, 40, 60, 80, 100, the absent ring 120 (whose sole representative on earth is that the apex of the defining 12:35:37 triangle lies on the perimeter of this ring,), and the two outer rings of perimeters 140 and 160 megalithic yards.
These above ring lengths form another set of smaller measurements relating to the cursus and Woodhenge and these also follow an initial sequence of small and related numbers, followed by a supply of convincing noughts after those simple leading numbers – multiples of ten. In other words, they too are similarly presented in integer lengths of megalithic yards raised by powers of ten.
This numerical arrangement does not resemble coincidence, does it? And neither does the 12:35:37 Pythagorean triangle that Thom identified as defining the geometry of Woodhenge’s complex design, whose unit length is its perimeter length (42 megalithic yards) divided by 12+35+37 (= 84), which is an exact half of a megalithic yard.
FINDING THE SERVICE MANUAL
I believe that this kind of analysis has revealed a useful section of a one-time ‘service manual’ for the Stonehenge site. In Part One and Two of this article, the mean diameter of the Aubrey circle – or AMD – was shown to provide a common or ‘link’ unit between Stonehenge and Woodhenge, and it is helpful to our cause to note that this measurement is possibly the most accurately known dimension at Stonehenge, a datum measurement determined following a seemingly unlikely liason in 1973 between Alexander Thom (on theodolite and pipe) and the conservative traditionalist archaeologist Richard Atkinson (on cigarette holder, bayonet and resistivity meter). This duo determined the Aubrey circle’s mean diameter (AMD) to be 283.6 feet in diameter (Thom & Thom, JHA, 1974 op cit). They even became close friends- it can happen!
In Part One, the line connecting Stonehenge centre with Woodhenge centre was measured as being 10035 feet in length, and (because it appeared to have formed the length of the ’13 side’ of a 5,12,13 pythagorean triangle) this was subsequently shown to be ‘factorised’ such that,
10,035 feet = 13 x 2.722 x 283.6 feet.
This equation contains a highly significant detail that could be easily missed. The presence of 2.722 as a factor implies that the megalithic yard was a known unit of length and had been employed in the measurement. Rewritten, the equation is
3686.8 feet = 13 x 283.6 feet
1354.44 megalithic yards = 13 x 283.6 feet
The ratio 10,035 feet / 3686.8 feet = 2.72187 = the numerical value of the Megalithic yard
This ‘theme’ can now be taken further, because had the length of the cursus been intended to be 13,610 feet, (from its westernmost boundary to the centre of Woodhenge), then a similar equation to (1) above can be formed,
13,610 feet = 48 x 283.6 feet (to 99.994%).
or 5000 megalithic yards = 48 x 283.6 feet.
The Aubrey mean diameter (AMD) now makes its debut with regard to the metrology of the cursus, within an equation that contains a small integer number multiplied by 1000. It may be useful to note that the Aubrey mean diameter, expressed as inches, is 3403″, which, in day-inch counting or tallying, (or counting one inch for one day), is half the lunar node period (a time period which averages 6800 days). This is significant evidence, firstly because Fred Hoyles’ Stonehenge eclipse predictor relied on the lunar nodal axis being defined by the opposing Aubrey Holes, and secondly because in order to be able to predict eclipses in advance the lunar node period of 18.61 years (6800 days) has to be known (Hoyle, On Stonehenge , Freeman 1977, page 97). Hoyle was the cosmologist and leading astronomer of his day, and his book On Stonehenge he explicitly showed how the Aubrey circle, with its 56 holes (or markers) represents a ‘perfect’ minimalist design from which it becomes possible to monitor the positions of the sun and moon, and to predict when an eclipse may occur by tracking the lunar nodal axis.
Professor Fred Hoyle’s original assessment of the Aubrey circle was undertaken at the request by Glyn Daniel, then editor of Antiquity, who requested a review of Hawkin’s Stonehenge Decoded (Hutchinson, 1965), a book he loathed. Hoyle wrote back to inform Daniels that much of the astronomy in Hawkins’ book was both correct and very interesting. His review was subsequently published in Nature as a feature article, titled Stonehenge – An Eclipse Predictor (Nature, vol 211, pp 454-456). Hoyle had noted that 3 x 18.618 (years) = 55.854 (years), and this enabled a pair of ‘node markers’ to be used to track the celestial position of the lunar nodes within the 56 hole Aubrey circle [55.584 is 99.74% of 56]. The 56 markers also enabled the Aubrey circle to satisfactorily track of the celestial positions of the sun and moon.
Harmonically, the numbers 56 to 48 form an exact 7:6 ratio]
Day-inch Counting and Eclipses
The length of the cursus, manifested as a marked up rope where one inch represents one day/night period, (a day-inch counting device), now is seen to represent 24 lunar nodal periods of 18.618 years, because,
18.618 x 365.2422 x 24 = 163,202 Imperial inches,
(18.618 x 365.2422 = 6800.079)”, the lunar nodal period, and
6800″ x 24 = 163,201.9 = 13,600 feet x 12 = 163,200 inches = 200,000 Megalithic inches,
(to 99.999%)
It is surely now reasonable to suggest that the dimensions of the Stonehenge cursus are directly related to both Stonehenge and Woodhenge, and that this little understood monument (the cursus, although the nomination could equally well be applied to both Stonehenge and Woodhenge) was intentionally dimensioned to provide an astronomical computational system, based on rods and/or ropes that could ultimately predict eclipses, in addition to providing a workable soli-lunar calendar.
THE STONEHENGE AVENUE
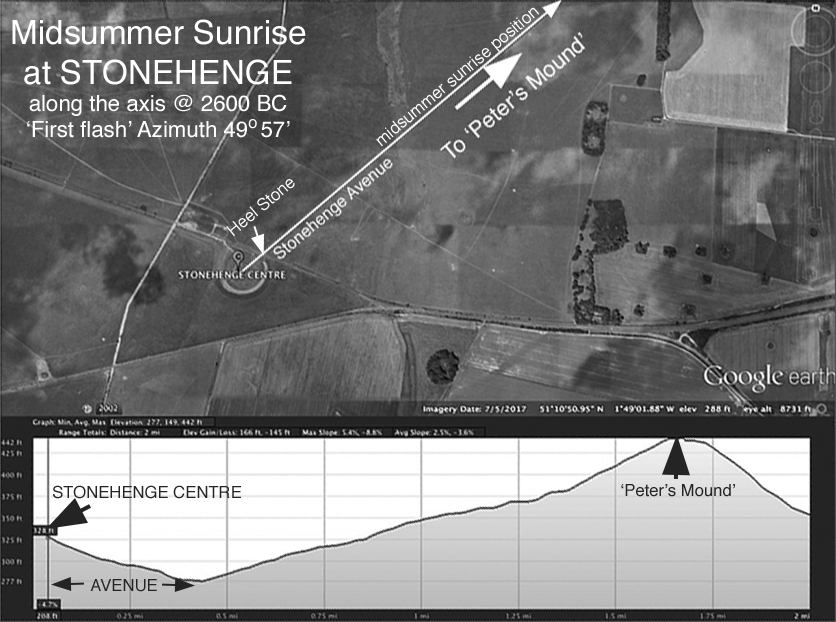
In addition to the Stonehenge cursus, the axis avenue at Stonehenge provides a second suitable location for the same kind of rope work outlined above and this monument has the advantage of lying on the Stonehenge ‘midsummer axis’, providing both a midsummer and midwinter ‘time check’. Using GPS, the avenue measures 1988 feet in length from the centre of Stonehenge to the point where it meets the centre of the path prior to it veering sharp right towards the river Avon. This same length is 730.5 megalithic yards, which is 365.25 megalithic fathoms (MF). On the Google Earth image below, the path off the right can be clearly seen just after the word ‘Avenue.’
Figure Four. The Stonehenge Avenue with its elevation profile (Courtesy Google Earth)
The length of the Stonehenge avenue can now be understood astronomically. By employing the megalithic fathom (MF), first named by Alexander Thom as a key unit in the design of stone circles and rings, the length of the avenue becomes 365.25 MF, which, as days, is the length of the calendar year (or solar tropical year to within 99.998%). Now, there’s something! The key fact is that:
The Stonehenge avenue was built aligned to that point on the horizon where the midsummer sun rose in and around 2700 BC and was made so that its length measured 365.25 megalithic fathoms, or one MF per day.
That the avenue was orientated to the midsummer sunrise has been known since 1740, when Stukely noted the fact that the axis of Stonehenge and the avenue leading from it are directed to the north-east ‘where abouts the sun rises when the days are longest‘. In his book Stonehenge, a Temple Restored to the British Druids he also quoted Plutarch, the Graeco-Roman Platonist who, along with other classical authorities from an earlier epoch, recognised the ancient practice of orientating temples to the position of the rising sun on their foundation day. A version of this practice of aligning temples was carried on, if somewhat disguised, well into medieval times and beyond as Christian churches were commonly aligned to the alleged birthday of the saint to whom the monument was dedicated or consecrated.
This great chronicler of his time, William Stukely, also noted a collection of regularly spaced stones along the banks of the avenue at Stonehenge. These stones have apparently vanished and no measured plans of these stones, by Stukely or anybody else, appear to exist. If ever stone holes were to be positively identified along the Avenue, these could provide further confirming evidence (or not) of the level of astronomical knowledge that was extant during the construction of the Avenue.
A NEW STONEHENGE STORY EMERGES
Something fresh can now enter the existing collection of Stonehenge stories. This new story draws far more on the fundamental data of measurement and far less on myths and legends. The key features at Stonehenge that relate or connected to observation of the length of the solar year is the Heel stone and the axis of both Stonehenge and its avenue. In old Welsh Ffriw yr Haul means ‘The ascending of the sun’, which goes a long way to explaining the origin of the somewhat unrealistic legend of the Friar’s heel, because the more modern appellation above is pronounced almost like the Old Welsh phrase. The fresh revelation is now that from the centre of Stonehenge to the right angled bend at the termination of the avenue measures 365.25 paces (Megalithic fathoms) in length, and that this unit of length was independently identified as being a megalithic unit within a family of megalithic units itself identified independently by Alexander Thom (1967, 1978).
How did we ever come to miss this wonderful connection for so long? Well, one reason could be because most archaeologists and even archaeoastronomers decided that Thom was completely wrong about his megalithic family of measures, and ignored them thereafter. It was, after all, Clive Ruggles, the man who held the only ever Chair in Archaeoastronomy in Britain, who pontificated in Astronomy before the Telescope (edited by Christopher Walker & Sir Patrick Moore) that,
‘There is no evidence for the use of astronomical observations for practical purposes such as determination of the time of year.’
The sad fact for anyone who ever believed this statement, or wanted to believe it, is not that the megalithic fathom reveals it to be untrue. It is that Ruggles pointed them away from even looking for such things. The lesson to be learned here is surely that ‘absence of evidence is not evidence of absence‘. Here we have found evidence: the midsummer sunrise calendar connection, stored forever within that dead straight length of the Stonehenge Avenue, is also of an appropriate length that corresponds directly to the length of the solar year, in days. But this evidence keeps on giving, for no other unit but the Megalithic fathom reveals this match between the length of the solar year in days and the length of the Stonehenge avenue, originally aligned to the midsummer sunrise angle. The new evidence eloquently informs us that this was intentionally so.
This discovery informs the researcher that the builders of Stonehenge had deliberately used this known and human measure, that in modern metrology would be called a pace, (a pace is two 2.722 ft steps, or 5.444 feet in length,), in order to numerate the number of days between each summer solstice. The Avenue thus enabled them to pace the year, and create a space or ‘diary entry’ for each day in the current year. One wonder’s what they ‘wrote’ or recorded in that diary – astronomical events, may one dare suppose?
So, here is some really good evidence supporting ‘the use of astronomical observations for practical purposes such as determination of the time of year‘. It is Ruggles and his statement that ‘the idea that distant horizon features such as notches could be used to pin-point the motions of the sun and moon to within minutes of arc‘ that can now be discounted.
[It should be noted that if the cursus length were 13,600 ft (99.92% of 13,610 feet)) then compared to the 1988ft length of the avenue, it would be 6.841 times longer, which is also 3400/497 and that 6.841 x MY = 18.618. The number of days in half a nodal cycle is 3,400 days.
This connects, in simple metrological terms, the astronomy of the lunar node cycle of 18.618 years, with the cursus length.]
There are other important connections to come. To discover these it is necessary to understand how a different type of monument recently discovered in a different location connects directly with the above newly revealed relationships linking the various major component monuments of the Stonehenge landscape. The next stage of this story therefore involves a remarkable and previously unrecognised monument in West Wales, one that has survived in good enough condition to be measurable with great accuracy.
THE LINK TO THE BLUESTONE OUTCROPS
A Visit to the Preseli Hills
Site 1. CARNINGLI
[Latitude 51*N 59″ 59″; Longitude 4*W 49′ 26″]
Figure Five. Carningli Summit
The most prominent visual feature within the Preseli Hills is undoubtedly that of the rocky summit of Carningli. This long extinct volcanic outcrop consists of a prominent long ridge whose axis is aligned northeast – southwest. At just 1070 feet AMSL, it is hardly a mountain, yet the rocky nature of the outcrop and its conical shape when viewed from the north or east of the Preseli Hills makes it appear much more impressive, more resembling a mountain than a mere hill (see photograph above).
Amongst the chaotic layers of volcanic rock along the summit ridge of Carningli can be found a anomalous flat seat or ‘throne’ that faces the north-east towards Cemaes Head (see Figure Five, above, where a white arrowhead marks its position). It is from this ‘throne’ that the observation of the St Davids Alignment is made (see Bluestone Magic, 2010), with Carn Briw, the dark ‘spike’ on the nearby horizon on the photograph (below, Figure Six) acting as a nearby foresight that indicates the notch between the twin peaks of Carn Llidi and Penberi (the grey peaks either side of Carn Briw)) near St Davids providing a distant foresight that once marked St David’s Day (prior to the calendar changes of the eighteenth century). Today, this alignment marks the setting sun on February 18th (in the spring).
Figure Six. The ‘Throne’ on Carningli Summit
I have observed this alignment over many years. From the ‘Throne’ it is possible to observe the track the number of days in the solar year. It also shows clearly, year on year, the quarter of a day that is added to the annual integer value of 365 for the (almost) true length of the solar year. Counting the number of days between observing this sunset one easily can observe the approx quarter of a degree shift between consecutive years, and that the fourth count always returns 366 and not 365 days. From this solar observatory it is perfectly possible to evaluate the length of the year as being 365 and a quarter days , or 1461 days in four years. This is as accurate as our current calendar.
One can identify many ancient sites along the length of this alignment, suggesting its continuation of use well into the late middle ages, when much of its length became embroiled and integrated into the once highly favoured and well trod Pilgrim path to St Davids.
Site 2. CRUGIAU CEMAES
[Latitude 52*N 02′ 28″; Longitude 4*W 44′ 06″]
The photograph below shows Carningli summit viewed from the trig point on the summit of Crugiau Cemaes, a second high spot renown in the area as a viewing platform, and recently being re-classified from a Bronze Age to a Neolithic site. In the late 1950s much of the site was seriously damaged by a local farmer using a tractor to demolish the tumps and thereby rid his land of rabbits.
Figure Seven (a). Carningli Summit from Crugiau Cemaes
This impressive elevated site is marked on the OS map as a view-point (sheet 145, Grid reference: SN125145). To visit the site, take the A487 trunk road from Cardigan towards Fishguard. After about 3 miles turn right to Nevern on the B4582. After a mile valley cuts through the hamlet of Glanrhyd, and a further 2 miles on, at the top of a long upwards hill, the monument is found located on the right, where a motley collection of barrows and an OS Trig station can be seen on the skyline. A car-park and lay-by are provided, and a gate leads to a public footpath, a three minute walk then takes the visitor to the summit and perhaps the most spectacular and often most elemental view of the Preselis and its coastline (see photograph above). The photograph below, taken from Ysgol Hen in Glanrhyd gives a good account of the visual prominence of the two main remaining ‘tumps’, the right hand one sporting its OS trig point.
Figure Seven (b). The Tumps of Crugiau Cemaes.
This site offers a view of the entire northern side of the Preseli Range of hills, from the eastern figurehead ‘mountain’ Frenni Fawr westwards to Carningli and beyond, to further smaller and less conspicuous outcrops, Carn Enoch and Garn Fawr. The prominence of Crugiau Cemaes was commented on by Pembrokeshire archaeologist Richard Fenton (1746-1811) who noted that the site could be seen from the coast at Aberystwyth, about 40 miles distant. On a clear day one can do a little better than this, as from Bardsey island both Crugiau Cemaes and Carningli can be discerned, at 50 miles range.
Site 3. LLECH Y DRYBEDD – the ‘big slab on a trivet’
[Latitude 52*N 03″ 16″; Longitude 4*W 46′ 18″]
Figure Eight. Llech y Drybedd, with Carningli Summit in the background.
Llech y Drybedd is one of the most significant sites in the Preselis. Work on the astronomy of this site has revealed its axis of symmetry to be aligned to the midsummer sunset around the date of its construction, which currently is set at around 2,850 BC. This dolmen is also a backsite for observing the midsummer sunset over Lughnaquilla mountain, in the Wicklow Mountains in Ireland, which are occasionally visible at 90 miles range, when certain atmospheric conditions are suitable.
From the top ridge of Crugiau Cemaes, looking towards the coast, there is a second ridge, along which can be made out a significant dolmen, known locally as Llech y Drybedd, or sometimes Llech y Tribedd. It is at the same height above sea level as Crugiau Cemaes, at 612 feet.
When viewed from Crugiau Cemaes trig point, Llech y Drybedd marks the minor standstill moon set in the north, at an azimuth of 300.5 degrees, with Llech y Drybedd providing the horizon marker. A second henge site at Gaer, on the Felindre Farchog to Moylgrove road, provides the backsite for the major standstill moonset through Llech y Drybedd, the horizon foresight, at azimuth 319.5 degrees. I have personally observed, recorded both events over the past thirty years making the required corrections for the change of obliquity. There are archived web articles on this site and also on www.skyandlandscape.com, as well as a fuller account of the astronomy of this remarkable dolmen site in my 2010 colour guide to the West Wales monuments, Bluestone Magic (Bluestone Press, 2010).
Figure NIne. Crugiau Cemaes viewed from Llech y Drybedd.
JOINING UP THE DOTS
Using Google Earth, the lengths between these three sites can be easily and accurately determined. However, this was not how the importance of these sites was initially revealed. It was only after reviewing theodolite readings taken from all three summits over many years that suddenly the geometry that connects the three points was recognised, and suddenly made clear.
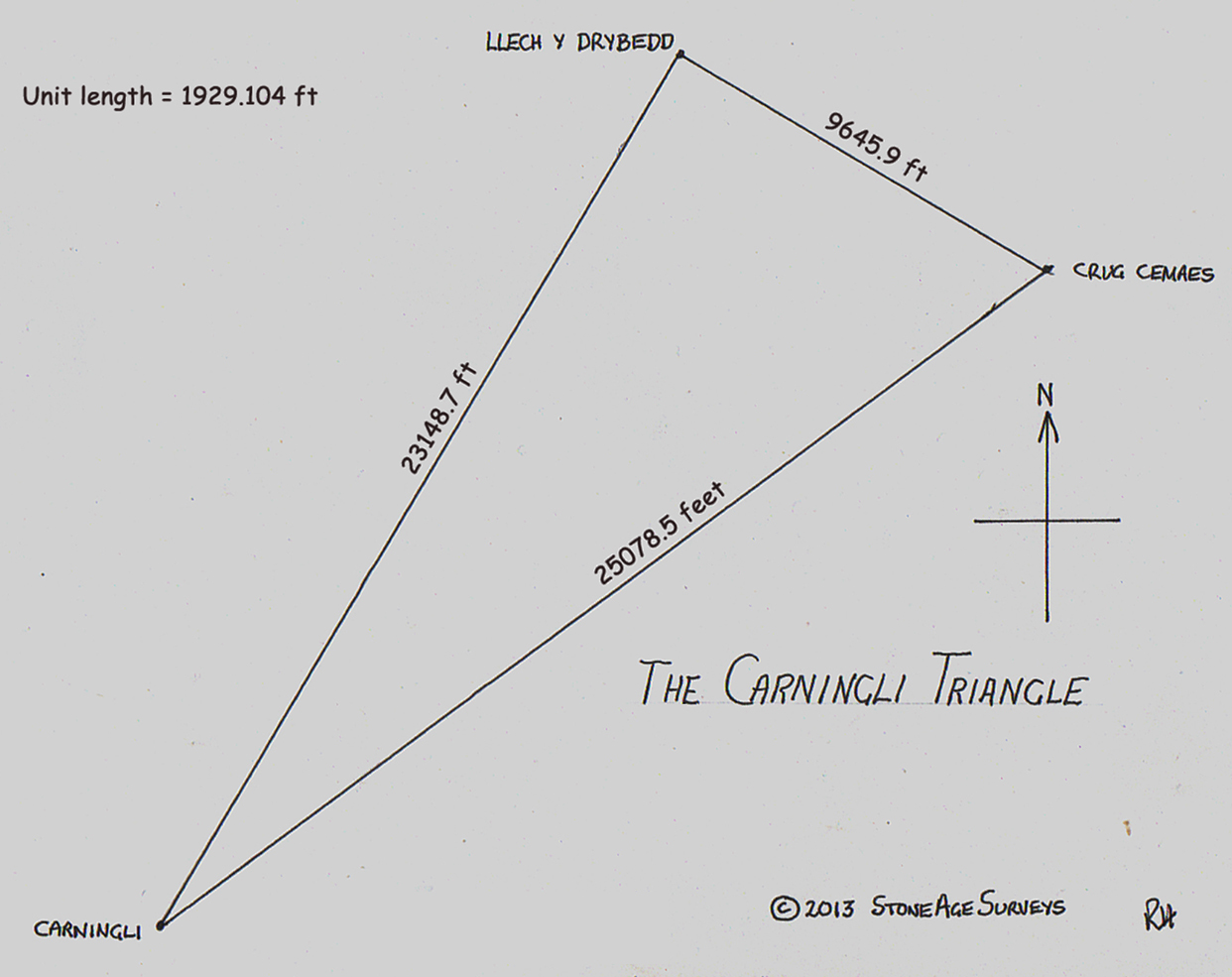
Firstly, a look at the original diagram, that followed my original survey, of the joined up sites – Carningli Summit, Crugiau Cemaes & Llech y Drybedd:
Figure Ten. The Carningli Triangle (the original 2013 diagram)
NOTES:
A. The three sites, Carningli summit (CI Throne), Llech y Drydedd (LYD) and Crugiau Cemaes (CC) form an accurate 5, 12,13 Pythagorean triangle.
B. The azimuth angles of this triangle, (obtained from a sun-shoot using a Wild T16 theodolite)) are
Azimuth of LYD from CI = 30* 27′ 00″
Azimuth of CI from CC = 233* 08′ 30″
Azimuth of LYD from CC = 300* 31′ 00″ (Minor moonset)
C. The internal angles of this triangle (measured using a Wild T16 theodolite), are
Internal Angle at LYD =90* 04′
Internal angle at CC = 67* 22′ 29″
Internal angle at CI = 22* 41′ 30″
[The ‘ideal’ internal angles of a 5, 12, 13 triangle are 22* 37′ 11″, 67* 22′ 49″ and 90* 00′ 00″].
C. The measured lengths between the three sites is as follows, taken from Google Earth:
Carningli Summit to Llech y Drybedd = 23,149 feet [12 side]
Llech y Drybedd to Crugiau Cemaes = 9646 feet [5 side]
Crugiau Cemaes to Carningli = 25,079 feet [13 side]
PERIMETER LENGTH (Σ P)=(23,149 + 9,646 + 25,079) feet
= 57,875 feet
UNIT LENGTH = (Σ P/ 30), [30 = 5 +12+13]
= 1,929 feet
This triangle is far too accurately defined (or configured) to be a chance coincidence of nature. The purpose of such a large landscape triangle connecting three summit points may by no means be clear at this stage. Nor is it clear if the unit length is significant or if that this length was purposefully chosen to fulfill an as yet unknown function. But it may be presumed that the accuracy of the geometry of this triangle makes it a vanishingly small chance that these sites came to be placed where they were placed by accident.
The data is largely presented in numerical form and, unlike almost all conventional archaeological data, it can be directly analysed and investigated by a non-specialist to answer such reasonable questions as;
Q1. Might the astronomical facts already established for these sites mean that somehow the triangle has a purpose relating to the solar year or to lunar cycles?
Q2. What unit of length were the designers of this geodetic shape employing in order to integrate or register solar and lunar cycles?
Q3. Is this triangle connected with the Stonehenge-Woodhenge triangle?
Q4 Is this triangle a lunation triangle (Heath, 1993 et al)?
Answers to these questions are forthcoming.
Answers to Q1 and Q2. There is indeed a connecting link between the unit length of this triangle, which is 1929.174 ft, and the lunar month of 29.53059 days. The ’12’ side of the triangle (23,149 feet) therefore happens to measure one lunar year in length, when measured in megalithic fathoms, and this is the lunar year of 354.4 days x 12.
1929.174 (feet) = Lunar year x Megalithic fathom
= 29.53059 x 65.3249
= 29.53029 x 5.444 x 12
= lunar month x meg fathom x 12
= lunar month x meg yard x 24
= lunar month x meg yard x 24
This equation both identifies and elucidates a connection between the unit length presumed chosen for the triangle (1929 feet) and the lunation period of 29.53059 days. If one day is here represented by one megalithic fathom, then the unit length of the triangle is one lunar year (354.36708 days x 5.444 feet)
The Lunar Month was perhaps the most important astronomical constant of all to the megalithic culture – a twelfth of the time period of the lunar year of 354.36708 days. It is here found embedded within a prehistoric 5, 12,13 Pythagorean triangle that was designed using an independently discovered (by Thom) prehistoric system of metrology.
Next to the solar year and the four seasons, the lunation period provides the strongest rhythm, in the music of the sun, moon and earth system. It is a rhythm all living creatures on the earth dance to, synchronous with the earth’s tidal cycles, both telluric, chthonic and oceanic, and synchronous with the human menstrual cycle.
Answer to Q3. The Preseli 5,12,13 triangle is found to relate directly with the Stonehenge-Woodhenge triangle. Although no right angle point appears to be marked on the landscape today at Woodhenge, the ’13’ side is sloping at the exact angle with respect to an east-west line in order to define a 5,12,13 Pythagorean triangle. It is not incorrect to assume the intention that the Stonehenge-Woodhenge line was intended to form the hypotenuse of a 5,12,13 triangle. and not just for this single reason, as explained in part I and part II of this tryptych of web articles on the matter.
The Carningli triangle follows this set of rules, for its ’13’ side is angled such that it is coincidental with the hypotenuse of a second triangle, a large 3,4,5 triangle, between Carningli summit and standing bluestones stones scattered around the farm at Pont Gynon, once the right angle point. Here, because the right angle point is not very clearly defined with the curtilage of the farm, the unit length is found from the hypotenuse alone, as 25,079 feet divided by five, which is 5016 feet, or 921.354 Megalithic fathoms This is therefore 2.600 times the unit length of the 5-12-13 Carningli Triangle.
THE PRESELI-STONEHENGE CONNECTION
A further significant factor remains to be discussed that seals the importance of the connections above. It is this: If completed, the perimeter length of the Stonehenge-Woodhenge triangle would have been identically matched to the length of the ’12’ side of the Preseli triangle, both at 23,149 feet. This makes the scaling between the relative sizes of the two triangles equal to 2.5 :1, or 5:2.
We here have powerful evidence supporting that these two triangles were the result of the same original cultural impetus.
Answer to Q4. Furthermore, the Preseli triangle still contains a well known megalithic monument within its perimeter that enables the construction of an inner 3,4,5 triangle to defines the 3:2 point. This is covered in detail with photographs within Proto Stonehenge in Wales (Heath, Bluestone Press, 2014), available via the book section of this website. This site, known as the Trefael stone provides, via a 3,4,5 geometry from Llech y Drybedd supplies the required 3:2 point to identify the Preseli Triangle as once having been understood and therefore used as a lunation triangle. This is an extra twist on the lemon!
Earlier, the Stonehenge avenue was found to support another example of astronomical and metrological integration, that supported the already identified possible connections for which the Stonehenge – Woodhenge – Cursus complex provided key component parts. Had the builder’s intentions been to connect the centre of Stonehenge to the elbow in the avenue at 1988 feet, prior to it making a sharp bend to the right to the river Avon, then the simple act converting 1988 into units of megalithic fathoms in length reveals the length of the avenue as being 365.25 (days = MFs), where once again, one megalithic fathom is made to represent one day.
Length of avenue = 365.25 megalithic fathoms
= the solar year, calibrated 1 MF /day
The Stonehenge avenue revealed a second astronomical secret, for it was not only aligned to the midsummer sunset, but in the appropriate units of the day provided a daily or calendar diary along its length.
CONCLUSIONS & SUMMARY
It appears likely that a 5:12:13 triangle connecting the centre of Stonehenge to the intended centre of a new (later) building, which became Woodhenge, may have been part of the process of ‘laying the bearings’ prior to Woodhenge’s construction, this later monument being erected following the first phase of Stonehenge had been constructed. In addition the so-called ‘Aubrey’ centre of Stonehenge was only possible to establish, i.e. available, between the time the Aubrey holes were originally dug and the later process of defining the station rectangle some three or four centuries later.
The 13th part of the length that separates the centre of Stonehenge from the centre of Woodhenge reveals the unit length of the triangle, in whichever unit of length one fancies to measure it. While it is possible to measure in the relatively new metrological ‘god’, the shiny and officially sanctioned ‘safe’ unit – the metre, this unit is mute when applied here, and only obfuscates what is going on, revealing absolutely nothing.
Use of the metre places an unnecessary and unwelcome fog between monument and researcher. In more appropriate metrological units the unit length is 771.9 feet, which is 283.6 megalithic yards, a unit handily provided by Thom (see earlier) that he also found to the unit of length that was employed during the design and erection of Woodhenge. The foot is suitably ‘hot’ in this application, the megalithic scientist /researcher can be completely comfortable when using these two unit at these sites, for,
771.845 feet = 283.6 MY
= (283.6 x 2.7216) feet
[283.6 feet = Aubrey mean diameter (AMD)]
This kind of analysis and its conclusions have previously been dismissed as entirely unrealistic within our modern culture, a culture that has forgotten, intentionally or otherwise, its prehistoric ‘megalithic’ past, or has dismissed any possibility of a science of megalith building founded on an alternative model of Neolithic capabilities, as outlined in the above report. The analysis, its suggestions and ultimately their authors (examples include Lockyer, Thom, Hoyle, Hawkins, Michell, Newham and many others, including this author) have instead been routinely banished into ‘Room 101’ of archaeology, that place reserved especially for those they do not agree with, and who they name the ‘Lunatic Fringe‘. This time honoured option has been far easier for archaeology than having to embrace the proposed alternative reality of prehistoric intentions presented by the evidence presented above. It is, of course, the lazy option, the ‘no-changes here’ stance.
However, the triangles described here make this easy option no longer available. One does not have to be an archaeologist to evaluate the data presented here, nor to understand its treatment. The evidence presented is unequivocal and clear in its presentation, emerging from several remarkably accurate artefacts, whose dimensions and other qualities reveal not only that the present model of prehistory is incomplete, but also that this model, as presently presented to the public by archaeologists, has failed to understand the true capabilities of the culture that built them. The model is woefully incomplete, and our true prehistory remains denied to us.
The current model of the prehistoric past is therefore of no practical use to modern times, and the recent stream of available evidence, some of which is presented within this report, suggests both how and why this model must now be radically redefined. The effort offers great rewards to anyone who really is seriously looking to understand our lost legacy from prehistory.
Robin Heath,
written between April – July 2018
www.robinheath.info
www.skyandlandscape.com