PART TWO – A SPECIAL RELATIONSHIP
In Part One a single action began a process of investigation – I made a measurement of two physical realities. The first was the length of a line connecting Stonehenge centre to Woodhenge, centre, and the second was the angle of orientation that this line makes with respect to an east-west line, termed a co-azimuth angle. This second part of the article shows where that single action can lead a researcher into understanding presently unsuspected purposes within the designs of, in this case, Stonehenge and Woodhenge.
These two measurements revealed a set of functions or purposes which presently no other technique being applied by archaeologists appears to be able to offer. Megalithic science claims to be able to provide a skill set whereby it becomes possible to understand the long-forgotten rules or lost prehistoric science needed to fathom out the purpose or function of a megalithic design that has stood there waiting to be understood for thousands of years. This experience can and often does confer an awesome sense of privilege, and it can connect a researcher directly to their far distant roots, seeing directly into the mindset of their ancestors. Once a few and quite simple rules are understood, the design rules, astronomy, units of length and geometry originally applied by the original architect(s) and/or builder(s) of a megalithic monument can be revealed. This methodology is presently and sadly not recognised by mainstream prehistoric archaeologists.
The various techniques and methodologies by which this recovery process is brought about has been described in many of my books and articles, and in many other works by other relevant researchers in this field. The experiences which led me to be able to write on this subject are perfectly crystallized below, when investigating the relationship between Stonehenge and Woodhenge.
Measuring the Distance between Stonehenge Centre and Woodhenge Centre
I had measured the distance between these two henge monuments previously, and even the angle, in 2003, during the writing of The Measure of Albion (Bluestone Press, 2004, co-authored with John Michell (a facsimile is available in the USA under the title The Lost Science of Measuring the World, 2006, AUP). At the time this data became buried with a mass of other material had been gathered at the time. I had derived the length from the OS map coordinates, and this has since become the quaintly old fashioned way! Google Earth arrived soon after 2003, providing an astonishingly useful tool for this kind of work, although it can be fraught with dangers in this work unless backed up with site work on the ground. Google Earth, like the map, is not the territory. (adapted from Alfred Korzybyski, with apologies!). Researchers will need to recognise that the model of the earth (The Geoid) used by the British Ordnance Survey in making maps of Britain is coded OSGB36, whereas Google Earth uses WGS84 (World Geophysical Survey 1984.) Conversions from one system to the other are available on the web.
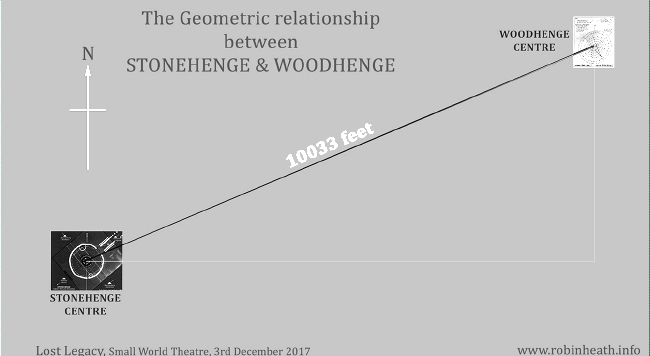
The 10033 feet measurement shown in the illustration above was taken centre to centre, using Google Earth. For Stonehenge, the centre was assumed to be that location where the diagonals of the 5:12 station stones rectangle cross each other. The corners of this rectangle were originally occupied by moderately large stones. They were set a few inches inboard of the Aubrey circle perimeter and asynchronous with its hole spacing (see diagram below).
More detail: Stone 91 now lies recumbent next to its original stone hole and stone 93 is a large solitary stump over to southwest of Stonehenge. There are two missing stations, 92 and 94, but fortunately the location of their original holes has been established (Atkinson, et al). The centre of the Aubrey circle, marked as explained above, is depicted below, on a useful diagram that also indicates the principal solar and lunar orientations at Stonehenge and the direction of Woodhenge centre, which remains clearly marked by a solitary drab concrete bollard.
Stonehenge centre to Woodhenge centre = 10033 feet ( ± 3 feet)
It is estimated that this measurement, from centre to centre, is accurate to better than plus or minus three feet of the value given above.
Maxing the Factors
Now look what happens when one discovers the component factors present within this number,
10033 (feet) = 13 x 283.6 x 2.722
The number 10033 feet can be represented by a tryptych containing three relevant numbers, each familiar to a student of megalithic science.
A).The number thirteen is inherently the numerical signature of the longest side length (hypotenuse) of a 5:12:13 triangle.
B). The number 283.6 is the mean diameter in feet of the Aubrey circle, established by professors Alexander Thom and Richard Atkinson, during their 1973 survey of Stonehenge. Each Aubrey hole was located by Atkinson by probing and resistivity testing, and its centre established and marked with a survey pin (Thom & Thom, JHA, 1974, op cit, see Part One).
C). 2.722 is the numerical value of the megalithic yard in feet, a unit that was originally discovered by Alexander Thom following two statistical methodologies prepared by the top Oxbridge statisticians of the time and based on analysis of the diameters of over 150 stone circles. (see Thom, MSIB, 1967, Chapter 5, and Thom & Thom, MRBB, 1978 , Chapter 4)
The point to point measurement of 10033 feet is also associated with an angle so similar to that of the apex angle of a 5:12:13 triangle that it may reasonably be assumed to have been intentional, part of whatever process of laying out the bearings from Stonehenge took place, prior to Woodhenge’s construction. This tends to support the present archaeological view that Stonehenge was the first of these two henges to be erected.
But did Stonehenge come first? This is an important question that must not be hurried in the answer. The earliest known structures in the immediate Stonehenge landscape are those three massive post holes which incongruously became known as the ‘car-park post holes’ during the 1970s building of the now defunct earlier Visitor’s Centre and tunnel. Their locations were eventually marked with large white painted circles of concrete.
Whether the Woodhenge site may or may not have been later adapted throughout its long history, it remains true that the earliest known building work on this henge site included some very large post holes.The post holes for Woodhenge indicate that the posts would have been extremely massive, requiring similarly large retaining holes, particularly if the assumed wooden posts were long enough to support a roof structure. Evidence exists, for Cunningham’s excavators indeed found that there were ‘deep ramps to all the holes in Ring III‘. Thom also states (Thom, MSIB,1968, p 75) that ‘if the posts were 2.88 ft (in) diameter the inside of the structure would be a perfect fit‘ (to the sequence of perimeter lengths, discussed in Part One).
But what if those sixteen holes in Ring III were originally not intended for wooden posts? It is by no means a done deal that they were, is it? Their diameter is well matched to many of the eighty or so bluestones that remain on the Stonehenge site today. Might Woodhenge have once housed a bluestone circle during the five centuries gap that currently haunts researchers into the origins of the bluestones. Woodhenge has been somewhat neglected over the years, a wooden Cinderella to its stoney sister, Stonehenge. Viewed sideway on, at ground level, it may resemble a load of bollards, but Thom’s surveyed plan (and Part One and the diagrams here) suggest that Woodhenge is far more interesting than that.
The Unit Length of a Triangle
For any size triangle laid out in two dimensional space, the unit length can be found by dividing the measured length of the perimeter, in any chosen unit of length, by the number of ‘units’ in the perimeter. For a known and accurate 5:12:13 Pythagorean triangle, the perimeter units total thirty, the sum of the side lengths [13+12+5]. For the triangle under investigation, the perimeter length totals 23,153 feet and the unit length becomes that value divided by 30, (see below).
Because the apex angle is negligibly different to that of a 5:12:13 triangle, the unit length can also be derived simply by dividing the 13 side length by 13. But this answer assumes that the 5:12:13 triangle is exact, and geodetic triangles laid out on the ground are almost never exact. However, for this example, on flat territory and over a small area, one would expect the unit length derived from the 13 side alone to be extremely closely matched to that derived from the total sum of all three lengths of this triangle, measured along the ground.
The two side lengths shown in red (on the diagram above) were measured using Google Earth. As an exercise, the reader may like to determine the difference between the unit length derived from the ’13” side alone and that determined from separate measurements taken of all three sides using Google Earth.
There is no substitute for being on site. Walking around this location shows that there is no surface sign that a right angle for this triangle was ever permanently marked, or monumentalised directly, although its location is strongly suggested by the geometry and metrology. A good place to dig, perhaps, but not, not ever, by other than qualified archaeologists who have the required blessings of EH and WHO.
For this example, the best estimate for the unit length is that derived from the ’13’ side alone. The 13th part of that length separating the centre of Stonehenge from the centre of Woodhenge becomes the unit length of the triangle, in whichever unit of length one chooses to measure it with. In feet it is the product of 283.6 and 2.722 , which is 771.77 (feet).
Unit length of the ’13’ side of the triangle = 771.77 feet
But this is also 283.6 megalithic yards (771.77 feet / 2.722 feet), numerically the mean Aubrey Circle diameter expressed in the larger unit of the megalithic yard, instead of the 283.6 feet (mean diameter) of the Aubrey circle. The three factors revealed above can now reduce to just two, and the length 10035 feet is seen to contain 13 lengths of 283.6 megalithic yards.
The 10035 feet distance connecting Stonehenge (centre) and Woodhenge (centre) is thirteen ‘super-Aubrey’ circles… (if you like)!
10035 feet = 13 x 283.6 megalithic yards
The Perimeter Length
The perimeter of a 5:12:13 Pythagorean triangle can be estimated by multiplying the length of the 13 side by 30/13, as shown above. This delivered 23,153 feet or 8,505.9 megalithic yards. The perimeter may also be measured using Google Earth for each of its three sides, and this presents an almost identical length, at 23,151.8 feet.
In Part Three, the consequences of this research will make it possible to recover yet more useful information from the designs of Stonehenge and Woodhenge, taken together. And we will then make a journey to the Preseli Hills of West Wales, where interest widens way beyond those outcrops that have proved to be the source of many of the Stonehenge bluestones.
Additional Notes : It is fortunate in this work that the foot and the megalithic yard have remained clearly defined and recogniseable units of length. Thom’s megalithic yard became recognised during modern times in Megalithic Sites in Britain (Oxford, 1967). Metrologist John Neal, in various metrological publications from 2000 onwards, proposed that the megalithic yard should more correctly have been named a megalithic step, being 2.5 times the length of the foot from which it derives within the traditional system of metrology, and not three times that length (a yard).
Neal identified the foot from which the megalithic yard derives to be the Geographical value of the Belgic foot (1.08617 feet). The root value of the root Belgic foot holds a ratio of 15:14 with the ‘root’ value of the English foot.
Similarly, Thom’s megalithic fathom (5.44 feet = 2 megalithic yards) would be better termed a pace, but Thom’s megalithic rod, (6.805 feet = 2.5 megalithic yards) sits comfortably within the canon, because a rod can be a double royal cubit, here based on a royal cubit whose single length is 3.403 feet.
In comparison, the inner and outer diameters of the sarsen circle accurately measure 28 and 30 double royal cubits at geographical value (3.4757485 feet), respectively.
Robin Heath, December 2017 StoneAgeSurveys skyandlandscape.com